비선형 포지션의 리스크 측정

   포지션 가치와 시장지표(market rate)간의 관계가 비선형인 경우 분석적 방법과 몬테 칼로 시뮬레이션 방법으로 VaR를 측정함

 

1) 분석적 방법(analytical method)

 

분석적인 비선형 VaR 측정방법으로는 델타추산법과 델타-감마추산법이 있음

 

□ 델타 추산법(delta approximation)

 

델타추산법은 선형모델을 통해서 옵션가액의 변동액 추정에 이용됨

 

ㅇ 델타(δ)란 현물 환율에 대한 옵션가격의 1차 미분을 의미

 

분석적 방법으로 VaR를 측정하기 위해서는 포트폴리오의 수익률을 먼저 산출하여야 하며, 독일 국채의 1년 현금흐름 및 a put on the DM/call on the U$로 구성된 포트폴리오의 수익률이 아래와 같을 때

 

분석적 방법으로 VaR를 측정하기 위해서

 

ㅇ 포트폴리오 수익률이 정규분포를 이룬다는 가정하에 95% 신뢰구간에서의 VaR은 다음과 같음

 

 

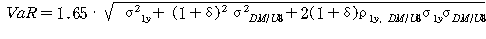
VaR

 

ㅇ 1일 VaR를 1주일, 10일 등으로 확대하는 방법은 “기간의 제곱근 법칙”을 이용함(σt = σ1․√t)

 

□ 델타-감마 추산법(delta-gamma approximation)

 

델타추산법은 환율변동이 안정적일때 정확성이 높으나 극한적인 상황에서는 정확성이 훨씬 떨어지는데 그 이유로는 환율가치와 옵션가격간의 비선형관계를 선형관계로 추산한데 기인함

 

ㅇ 이런 문제점을 해결하기 위하여 현물환율 변동의 비선형 효과(수익율의 제곱)를 반영한 감마조건을 추가함

 

ㅇ 감마조건을 반영한 포트폴리오 수익률 수식은 다음과 같음

 

감마조건을 반영한 포트폴리오 수익률 수식

ㅇ 감마조건은 rp분포의 비대칭성(skewness)을 초래하여 정규분포의 가정이 더 이상 성립되지 않기 때문에 95번째 퍼센타일 VaR(1.65 × rp의 표준편차)를 계산할 수 없으므로 비대칭성 효과를 반영할 수 있는 적절한 승수(-1.65에 상응한 숫자)를 도출할 필요가 있음

 

ㅇ 즉, 4가지 모멘트(rp의 평균, 분산, 비대칭성 및 첨도)를 계산하여 rp 분포의 5번째 퍼센타일을 계산함

 

2) 몬테칼로 시뮬레이션법

 

정규분포 및 대칭이 아닌 손익분포의 포트폴리오는 분석적 VaR 측정에 한계가 있기 때문에 변동성과 상관관계 추정치로 작성된 다양한 시나리오하에서 모든 금융상품이 시가평가되는 완전평가모형(full valuation)임

 

ㅇ 몬테칼로 방법은 다음 3단계 절차를 밟아 분석함

 

① 시나리오의 작성(scenario generation), ② 포트폴리오의 가치 평 가(portfolio valuation), ③ 요약(summary)